Dynamic Temperature Sampling (for better Creativity & Coherency in Large Language Models)

Introduction

Why would you need a Dynamic Temperature?

Typical attempts to make language models more varied and creative through higher temperature values might not work as you'd expect, due to the fact that higher temperatures disproportionately impact high confidence token generations. This is especially a problem for weaker language models that have less of an innate ability to 'course correct' when an awkward/bad token is chosen / less dramatic confidence in their top probabilities.
As a consequence, higher temperature values (past ~1.2) are rather difficult to use if you want your language model to output coherent & creative generations. A specific example of how higher temperature can introduce difficulties is in the case of adhering to programming language syntax, as they all have strictly defined rules. This can be an issue if you want an LLM to try a more 'creative' solution to a specific programming problem while still consistently adhering to the rules of the language; a static temperature isn't the most effective way to scale language model creativity.

What are the current best solutions to the problem?

Traditional approaches to prevent temperature from choosing unlikely tokens (the 'tail end' of probabilities) all attempt to tackle the issue by preventing the tail end from being considered at all. This comes with the issue of accurately determining the point in which a 'good' token is a 'bad' token, which will vary dramatically based on how the probability distribution is laid out. As a result, you're still having to compromise for either creativity or coherency when using sampler restrictions like Top P or Top K.
Approaches like Top A try to change where that cut-off is defined based on the top token probability, and are a step in the right direction, but still enforce a dichotomy for possible tokens where they must be considered 'good' or 'bad' rather than somewhere inbetween.

How would a Dynamic Temperature be implemented?

I propose a method that scales temperature dynamically to accomodate for these flaws based on the HHI of the probability distribution. We can do this by measuring the logits after running the softmax and then mapping a temperature value based on the measured HHI value for each discrete token generation. Thus creating a dynamic temperature that scales on the fly.
The hypothesis is that HHI (sum squared probabilities) is a helpful metric for scaling due to the fact we can roughly measure how 'concentrated' the language model's probabilities are, with heavy bias towards the top tokens implying less room for randomization (aka, lower temps). Here is a visualization of how HHI measurements tend to look.

What unique benefits would Dynamic Temperature introduce?

It would be easier to control / understand compared to existing approaches to align the creativity of generated LLM outputs. Unlike Mirostat, this would be 'context-free' as the context used would be the current probability distribution at any given time.
It would be more adaptable to different tasks without manually playing with hyperparameters.
Potential (currently unproven) improvements in creative problem solving ability.
There would be an inherent decrease in the necessity of limiting or cutting out tokens / external samplers in general, as outlier generations would be highly discouraged (the "tail end" would naturally be scaled out of the picture when the distribution implies a higher degree of certainty.) I'm hoping that Top P is the only other sampler that will be necessary for optimal results.
The current approach is to have a minimum temperature and a maximum temperature, as well as an exponent value that controls the power function that maps the HHI value to temperature.

This is a infographic I made to explain how temperature works.

Current Proposed Approach

HHI sampling is what is available in the builds mentioning 'Gini sampling', my apologies for the confusion. This is because it measures concentration of top tokens first and foremost. Specifically, it is calculating the sum of the squares of the individual probabilities and normalizing it.

HHI seems to be better at measuring confidence for the purpose of temperature mapping compared to Shannon Entropy, which was my last approach. I theorize that this is because HHI cares very little about the tail end of probabilities proportionally, as it directly measures the concentration of one or a few dominant 'players'. This makes it a good scoring mechanism for the dominance of top token(s) in the LLM probability distribution.

Here's is some real world data of the HHI measurements for ~500 token generations of two different tasks:

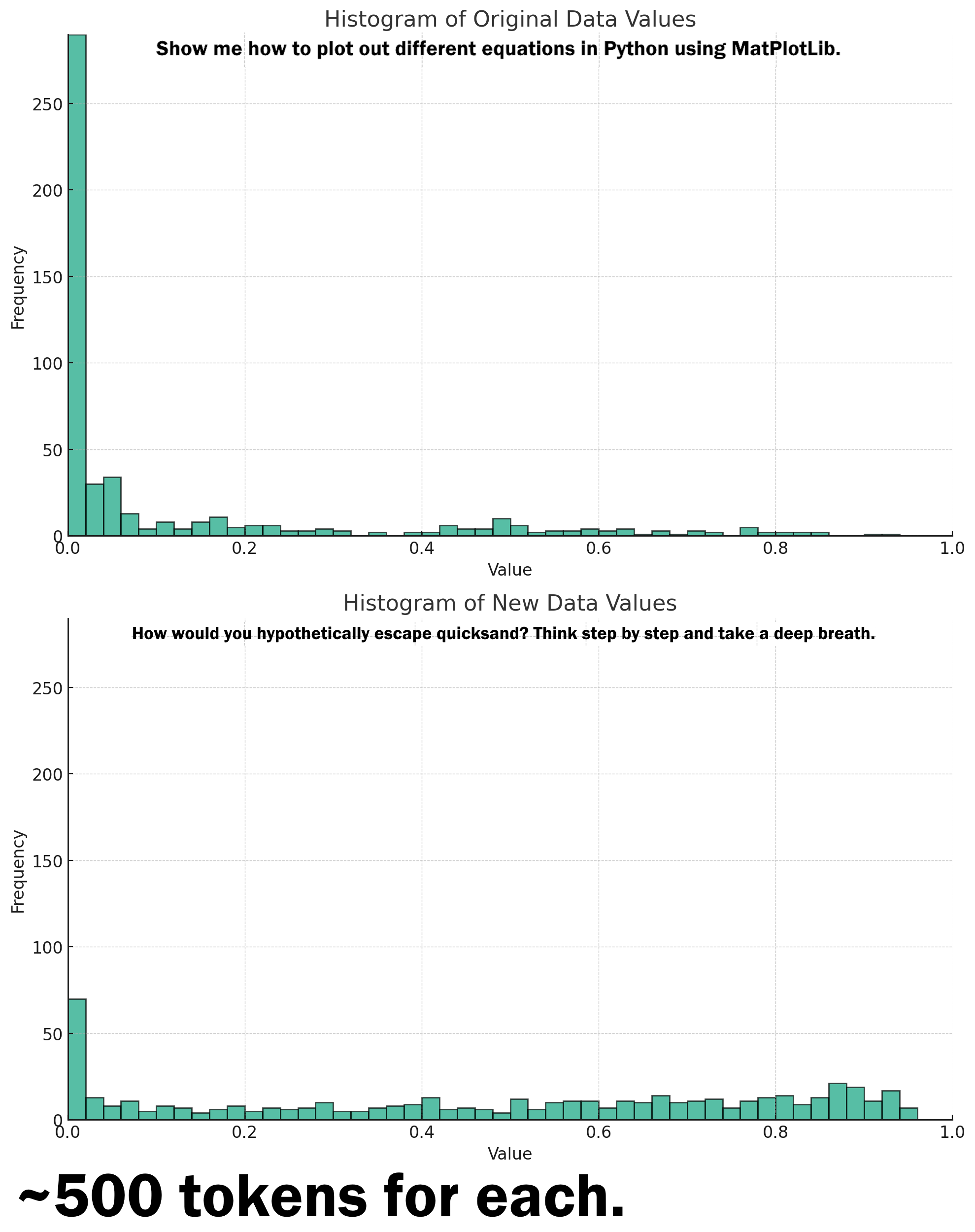
Past Approaches

Gini Sampling Clarification

This is a misnomer; I should have been calling it HHI sampling.

Entropy Sampling (mapped to temperature via Power Function)

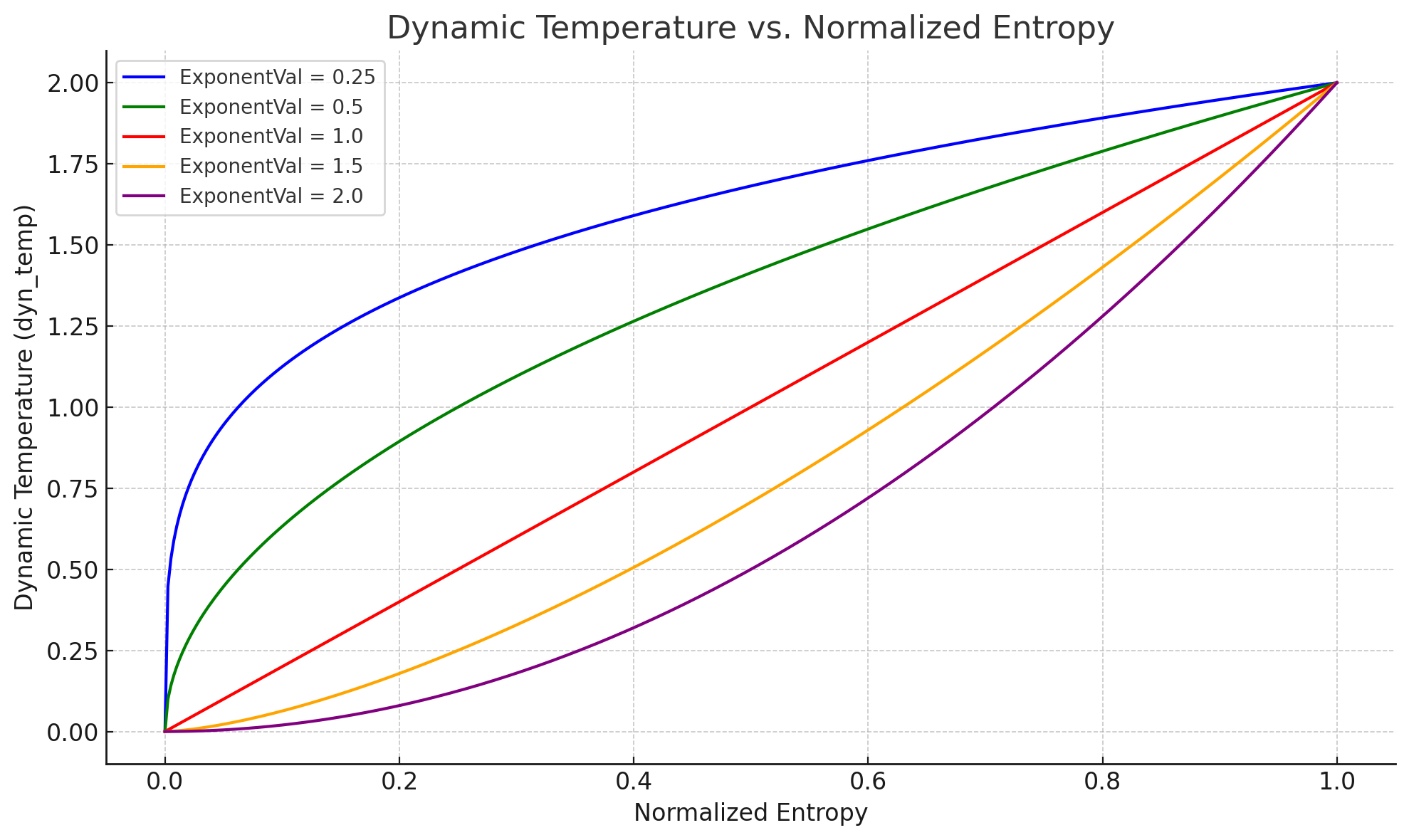
A power function that maps the measured Entropy to a range of temperature values (between your minimum temp of 0 and max temperature of 2.0), given an exponent value.

An infographic for shannon entropy in the context of measuring language model logits.

DynaTemp

Before I had the idea to measure Shannon entropy, I was using a sigmoid function mapped to the probability of the most likely token rather than factoring in the nuances of the entire distribution. This method still does pretty decently, but is most likely suboptimal (I've been told it follows the character better but can struggle with repetition). I have two test builds I posted of koboldcpp that have this (nicknamed DynaTemp): https://github.com/kalomaze/koboldcpp/releases