An Alternative to Test-Time Scaling
Exploring conditional computation and dynamic depth in language models.
Contents
Conditional Computation
I am interested in the idea of retrofitting existing language models to different architectural formats to better take advantage of conditional computation.
Most MoE literature tends to focus on creating a more efficient way to pretrain models at scale, but it's rarely used to create models that are capable of changing their computational width/depth dynamically. While there is existing literature on "layer skipping" (Mixture of Depths) and early exiting, I will mainly be focusing on two papers (later on) in this which I view as having the most promising implications.
But before that, let's provide some background.
The Distinction between "Width" and "Depth"
When pretraining a typical dense Transformer model, you are stacking many layers one after the other. For example, Llama3 8b has 32 layers, and uses about ~250m params for each layer.
There is a balance between the width/size of each individual layer, and how many layers you actually have in total (which sets a hard cap on the effective depth).
The "optimal layer count" is not something that has been thoroughly tested in the literature, which is a surprise to me since we know that:
- Deeper models tend to generalize better than wider models, but tend to memorize worse (given the same "parameter budget", you can distribute width vs depth differently).
- Some types of calculations require a lot of "depth", but not so much "width".
The simplified high level abstraction I have in my head that distinguishes "width" from "depth":
- Width defines, "how many possible simultaneous transformations can the model consider at once at any given point?"
- Depth defines, "how many unique transformations can be done before the model is forced to 'settle' on a particular set of predictions"?
Obviously, you need both of these things; you can't aggressively favor one over the other. If you are only computing 2 million parameters at a time for ~4000 layer operations, you will be spreading your model's capacity too thin; and if you are computing 2 billion parameters at a time for an 8b model for ~4 layer operations, you are not going to be able to make a bunch of individual small transformations that individually and precisely account for small changes in the contextual state.
Thin & Deep / Wide & Shallow
Some problems favor individually thin but deep computations, and cannot be parallelized as effectively.
An example of a "thin and deep" problem:
- arithmetic operations for computing a particular large number.
This is thin and deep since it's a very focused operation, where branching in various directions will not achieve a better solution.
However, other problems do seem to favor shallow, "thick" computations.
An example of a "wide and shallow" problem:
- applying the same operation in parallel to various parts of the sequence (i.e. retrieval, search, "accessing" memorized information)
Ideally, the model could do both of these things when contextually appropriate; but our architectures tend to be "one size fits all".
o1 / "Test Time Scaling"
o1 type models (dubbed "Reasoners" by OpenAI) are unique in that they specifically employ Chain of Thought prediction to better chase verifiable "objective" rewards.
While CoT can help ground these models and help them learn from discrete decisions that either did or didn't work, we inevitably end up wasting a lot of the width in our computations by attempting to split up the depth of a much larger prediction into various tokens that slowly express a decomposed solution.

It attempts to scale the fundamental depth limitation away by adding more individual token steps; and while this can work, I believe that "one size fits all" architectures still lead to undesirable properties.
Think of it as scaling "depth" in a horizontal way, rather than in a vertical way; there's no way for an individual token prediction to become deeper.
This can lead to unnecessary, exceptionally redundant checks.
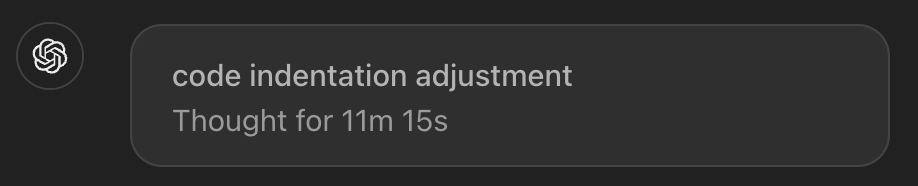
Just look at o1 pro taking ~11 minutes on code indentation for a large script:
What I am interested in is scaling "depth" vertically in such a way where:
- The model size only sets a hard bound on how many unique circuits there are, not how much computation each token is allowed to use (scaling computation per-token without making the model bigger)
- The model can learn to perform both kinds of computation (variable width or depth), rather than the architectural shape forcing a tradeoff between "deep" or "shallow" problems
Let's talk about those two papers I alluded to in more detail.
SMoE Dropout
- A paper published in 2023 pointed out that training a model on a progressive schedule where the activated width (low experts activated) starts low, but progresses to full capacity in a linear fashion, results in a model that generalizes to functioning conditional width computation.
- This was with respect to the MLP params, which make up ~80-90% of model computation. (Sparsifying attention is both possible and useful but would increase complexity of the architecture.)
- They used random routing for the width computation and did not make it learnable which proved to be more stable and resulted in a lower loss than routable MLP experts; fine-grained sparsity (128+ experts) resulted in the best performance compared to Mixtral style layouts of say ~8 experts.
MoEUT
- A paper published in 2024 which attempts to scale Universal Transformers in a way that uses sparse computation.
- The idea is to share all parameters in the model as much as possible, and use repeated sparse computation.
- Expert routing regularization is done across the SEQUENCE and not PER TOKEN for stability, and finegrained sparsity is employed for both attention AND MLPs
- Uses a new kind of normalization to keep the hidden state progression stable to train (in terms of magnitude), since a normal dense Transformer with discrete layers can learn to scale the output residual contribution in a relatively stable fashion.
- A compromise is used where two groups are repeated recurrently as opposed to a single group.
- They are able to use approximately ~40% of the equivalent computation of the baseline model via repeated sparse computation while beating the baseline in terms of perplexity; but there is no optimized kernel, so wall clock time overhead doesn't look very good atm
TL;DR
- SMoE dropout proves that models can learn to vary their computational width natively.
- MoEUT proves that models can learn to control "depth" as a controllable parameter that isn't tied to the model architecture itself, and allows it to be controlled by recurrently stacking two groups many times over (e.g, 2 groups with low width activations that are repeated 8 times instead of 16 discrete layers tied to the architecture itself).
What to do next?
Retrofitting a dense model into a MoEUT structure would require readjusting it to both sparse activation patterns and the repeated "horizontal" computation. This seems like it would be a much more involved process than trying to replicate SMoE dropout's "self slimmable" property where the desired width can be determined (or learned!) at inference time.
While I still want to look into this, I am thinking the smartest next step is to replicate the SMoE dropout model's ability to handle varying width sizes by training not according to a linear schedule, but according to multiple forward passes with different activation ratios, and targeting the original model's probability distribution for all the mentioned ratios as a proof of concept.
I think the easiest test for retrofitting an existing model to support variable computation (later on the plan is to make it conditional via some other heuristic, but we're not there yet) would be:
- Splitting just the MLP projections in a fine-grained fashion, via random grouping (i.e. ~256 experts for Mistral 7b)
- Doing Knowledge Distillation on the dense baseline according to various "k experts" configurations for ~10b tokens
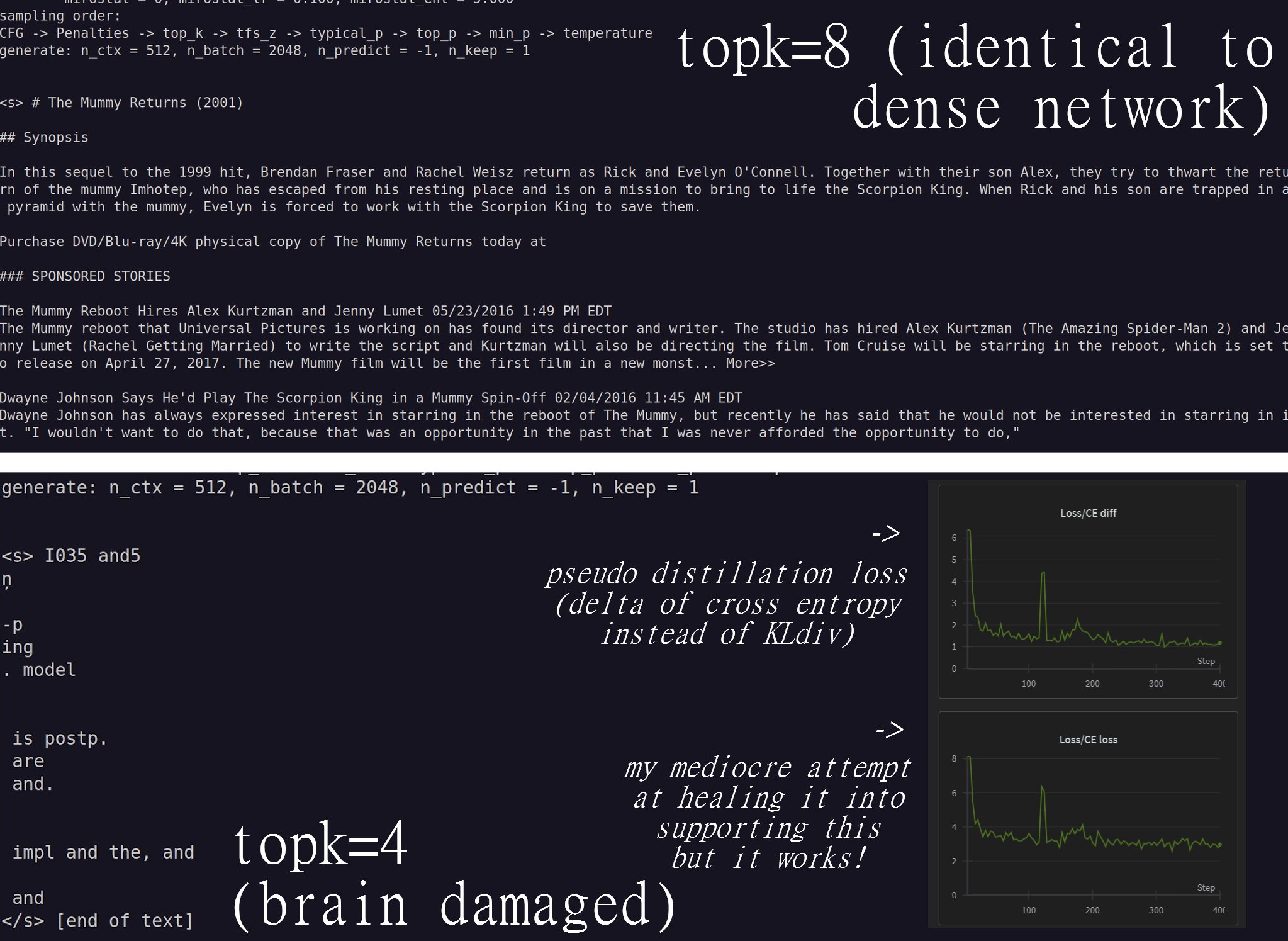
Here is a generic proof of concept showing learnable MoE routing (the kind that tends to be unstable) and a relatively low split of experts.
(I believe the training graphs were showing topk=8 over a topk=16 split, and the left side was an 8-way split test, sorry if this is misleading).
This test was no more than ~10 million tokens at best and on a fairly limited batch size.
My theory is that lacking fine-grained splits leads to very unstable routing by default.
14,336 divided by 16 = 896 dims randomly grouped together, that x 4096 = ~3.6 mil parameters randomly grouped together per projection.
So the next thing to ablate would be expert splits along the lines of say 256, which would look more like 56 dims (e.g. ~220k params worth of random grouping per expert) and as a result would likely heal far more effectively.
Proposed setup for the 7b test
Assuming 256 as the split ratio for a 7b layout, and assuming 128 H100s (16 nodes of 8xH100)
With frozen/non-learnable routing, assuming asynchronous training ala DiLoCo.
All would be targeting the same frozen dense model's probability distribution via Knowledge Distillation (KL divergence). We can use a randomly sampled subset of tokens, (ala how Gemma2 9b does it) if "whole vocabulary distillation" proves intractable memory wise.
How do we "learn" contextual compute allocation?
This is not an easy question to answer while still keeping batch level training "static" (when it comes to the computational graph).
However, Mixture of Depths shows that binary skipping of layers (through "routing around") can work.
This is something that needs to be ablated and tested empirically, but my first guess that a routed distribution of compute allocation over the whole sequence (ala MoD) could be used.

I envision something along the lines of "maximum recurrent loops" and that a "skip" (no computation) counts towards the maximum.
So, for example, if apostrophe token in the word what's gets skipped 50 times out of 80 total loops, it only sees ~30 actual computations throughout the whole forward pass. And there is a distinct possibility that the times it does get computed trend towards the lower end where less width is used.
This is something that needs more thinking and testing before I am confident about it but I'm sure there's a decent tradeoff somewhere.