Not this shit again

If you have been sent this link, it means some jackass on 4chan has yet again posted a thread with the above image. Whatever the thread's title and text were, they're going to be completely ignored. The thread will fill up to the autosage limit with guaranteed replies between people who think the answer is 1/2 and people who think the answer is 2/3. If you're unsure and just checking this link for a definitive answer, the probability is 2/3. This isn't up for debate, the problem isn't ambiguous. In fact, it might make a good problem for an assignment in a high school statistics class were it not so famous. But I know you. You're looking for a fight, and you're sure that the probability is 1/2. You just need to learn my reasoning so you can craft the perfect argument against it. Don't worry, I will show you my reasoning, but first I'd like for you to back up a bit.
You are in a slide thread
Let's question for a second the validity of this thread you are in. This question is posed constantly for several days at a time, with new threads being created after another tanks. And then they stop for a few weeks or months before popping up again. Nothing productive happens here, just a bunch of nerds arguing back and forth over a statistics problem. No one ever changes their minds either, because as it turns out, lots of people have cognitive biases that prevent them from changing their minds. We ignore evidence that contradicts our own narrative, and we actively seek out any evidence that confirms our viewpoints, giving it less scrutiny than evidence against us. We desperately want to be right because it hurts us to be wrong. And so we will fight, forever, over a meaningless problem.
And in the mean time, we will not be discussing other topics. Furthermore, due to the way 4chan threads work, we will be hindering the ability of other people to discuss topics. Every time a thread receives a post, if it has not hit the autosage limit, it is pushed to the top of the catalog, and pushes every other thread lower by 1. And every time a new thread is created, the thread at the bottom of the catalog is destroyed. By continuously creating new threads that rapidly attract new posters, other threads get indiscriminately swept away. If I were interested in preventing discussion on some current topic on 4chan, this is the type of thread I would make.
Or this is just a troll
There is of course a second possibility, which is that we are all being trolled. This shouldn't be much of a surprise, since troll threads have been commonplace on 4chan since time immemorial. But it would make it easier to understand why there are so many bad faith arguments. The person you are speaking to claiming that the answer is 1/2 (or perhaps offering a more absurd response, like 2/5) may know the real answer is 2/3, but he wants to keep you arguing. Wasting your time is a form of entertainment to him. And with a thread like this, he can waste a lot of people's time. Perhaps he doesn't even need to argue himself, because these threads practically guarantee replies. Why?
Statistics is unintuitive
If probability, expected value, and other topics related to statistics were easy to understand, casinos would not make as much money. One of the most especially unintuitive applications of statistics is conditional probability. So what is conditional probability, and why is it so hard for us to reason about? The definition is pretty simple: it's the probability of one event occurring, given that another event has already occurred. To make things less verbose, we may want to give names to these events as we explain them. We will say that B is the event whose outcome we already know. Meanwhile A is the event whose outcome we don't know, and we'd like to update the probability of it occurring, based on our new knowledge of B.
The problem with all of this setup, which makes the entire topic confusing to most people, is that both A and B occurred in the past. They were both random events, occurring with probabilities P(A) and P(B) respectively. We'd like to think that our knowledge of B's outcome means that the probability of that outcome is 1. We want to think that the outcome of everything is predestined. And perhaps that is true, but we are nevertheless uncertain about A's outcome. It too occurred in the past, and when it is eventually revealed, we will be certain that it could have only ever turned out in one way. But for now, we must find a way to cope with our uncertainty.
Bayes to the rescue
It turns out, there are a lot of cases in life where we have uncertainty about some event. Probability is our method of quantifying that uncertainty. Conditional probability is how we update that uncertainty. To calculate conditional probability, we turn to an 18th century English statistician named Thomas Bayes. For two events, A and B, he devised a well-known formula for updating the probability of A, given our knowledge of B. The term used in mathematics is the conditional probability of A, given B, which we write as P(A | B). Using the probabilities of A and B prior to our knowledge of B's outcome, Bayes Theorem states that:
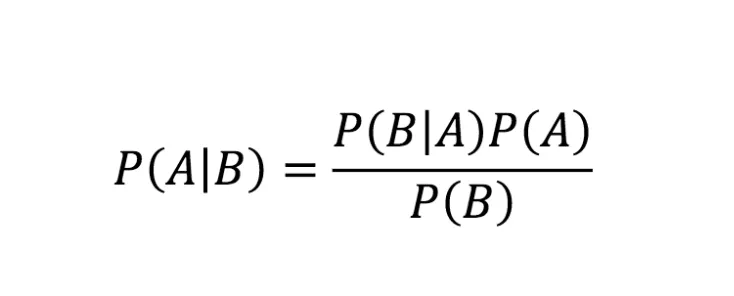
For our good old gold and silver ball problem, it's just a matter of figuring out A and B. We picked a random box, and picked a random ball from that box. We want to know the probability that the other ball in the box is gold. So first things first, the probability we are trying to update (A) is that the other ball in the box is gold. An easier way to formulate this is, that A is the event of picking the box that had two gold balls. We had three boxes we could have picked, all with equal probability (remember: we're not taking into account the evidence here, so even the box with two silver balls is fair game), so P(A) is 1/3. Now for B, we have to be a bit more clever. The evidence is pulling out a gold ball. But what event is that, pulling a gold ball out of a specific box? We don't know what box it is. So we might describe B as "pulling a gold ball out of any box that is picked". So for this, we consider that there are 6 total balls in all of the boxes, and 3 are gold, so P(B) is 1/2. That leaves us with just P(B|A). Now this, we can just say is 1. If you picked the box with two gold balls, there's a 100% chance you get a gold ball out of it.
Calculating all of this together, we get P(A | B) = P(B | A) * P(A) / P(B) = 1 * (1/3) / (1/2) = 2/3.
Simple enough. And we can even calculate the probability of the other two boxes. Our probability P(A) is not going to change no matter what the box is beforehand. But our probability P(A | B) is going to change because the likelihood, P(B | A) is now different. For the box with one gold and two silver, P(B | A) is 0.5, since we could have pulled gold or silver out of it. And for the box with two silver balls, P(B | A) is 0, since there's no way to pull a gold ball out of a box with just two silver balls in it. So given our evidence, we now have 2/3 probability for the box with two gold balls, 1/3 probability for the box with one of each, and 0 probability for the box with two silver balls. We understand intuitively that the silver ball box should have 0 probability, but how its probability is distributed to the two other events is what confuses us. It doesn't need to evenly go to all of them.
But what if I don't trust Bayes theorem
Here's a proof. It takes up half a page, and the only bit of extra math syntax you need to know is the set intersection symbol, which looks like an upside down U.